Fraction Division with Supports for English Learners
Teacher Guide
Getting Started with Diagrams
Why are mathematical diagrams part of the ADSEL fraction division lessons?
A primary focus of the ADSEL unit is on strengthening and extending understanding and problem-solving related to fraction division, especially through the use of diagrams. The unit addresses CCSSM standard 6.NS, Apply and extend previous understandings of multiplication and division to divide fractions by fractions and specifically, 6.NS.1, Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. At the end of the unit, students will be able to solve a variety of fraction division word problems and use number lines and tape diagrams to represent, reason through, and communicate about operations with fractions in real world problem-solving contexts.
Mathematical diagrams are important tools for supporting mathematical reasoning, problem solving, and communication. Diagrams are graphic creations that illustrate relationships among quantities. Examples of diagram types include number lines and tape diagrams. Diagrams are particularly helpful for exploring fraction division and underlying concepts of fractions. Diagrams help students solve division word problems by linking quantities and relationships described verbally in the problem to mathematical operations needed for a solution. Diagrams also support students to attend to the mathematical structure of the problem and to critically examine the “whole,” as typical student errors include incorrectly defining the whole. Diagrams help students identify what important elements are needed to solve a task as well as support students in their communication about their thinking. Some ways in which diagrams can support problem solving include:
- Diagrams can show quantities and relationships.
- Diagrams can relate quantities and relationships to the problem context. For example, in Lesson 3, a diagram can show how much soil is left after filling pots completely.
- Diagrams help students identify what important elements are needed to solve a task.
Furthermore, working to understand a student’s diagram can help a teacher understand a student’s thinking, and thus point to ways to build the student’s proficiency. This, we believe, is important for all students, but essential for students who are English learners (ELs).
Why emphasize diagrams for students who are English learners?
There is general consensus among mathematics educators that diagrams are useful tools for students, especially in middle grades. Diagrams are also central, if not essential, tools to widen ELs’ access to mathematical thinking and communication, enabling them to participate productively in mathematical discourse. When used as thinking tools and not just as tools for presentation, mathematical diagrams are helpful for the vast majority of students, with multiplier advantages for students who are ELs.
Diagrams present visual representations of the important quantities from a word problem; therefore, from the start, a diagram can free ELs to concentrate on reasoning about those quantities and their relationships rather than focusing on the words in the text.
Mostly, however, diagrams are beneficial to both ELs and their teachers because they are loaded with evidence of student thinking, which in turn can guide teachers toward questions that can advance student thinking. For example, consider this word problem that middle grade students may see: Jen went shopping for clothes. She spent $42 on a shirt, which was of the money she had at the start of the shopping trip. How much money did Jen have at the start? Suppose a student who is an English learner drew the diagram below, perhaps because she remembered what a fraction strip for looks like, but was unsure what to do next:
 The diagram presents evidence of the student’s thinking, which provides the teacher with visual evidence of what the student is thinking about. Possible teacher questions to elicit and advance this student’s thinking based on what is drawn include:
The diagram presents evidence of the student’s thinking, which provides the teacher with visual evidence of what the student is thinking about. Possible teacher questions to elicit and advance this student’s thinking based on what is drawn include:
- Can you show me the in the problem?
- Can you label the shaded part with a dollar amount?
- The total shaded part is $42. How much is in each of the shaded parts?
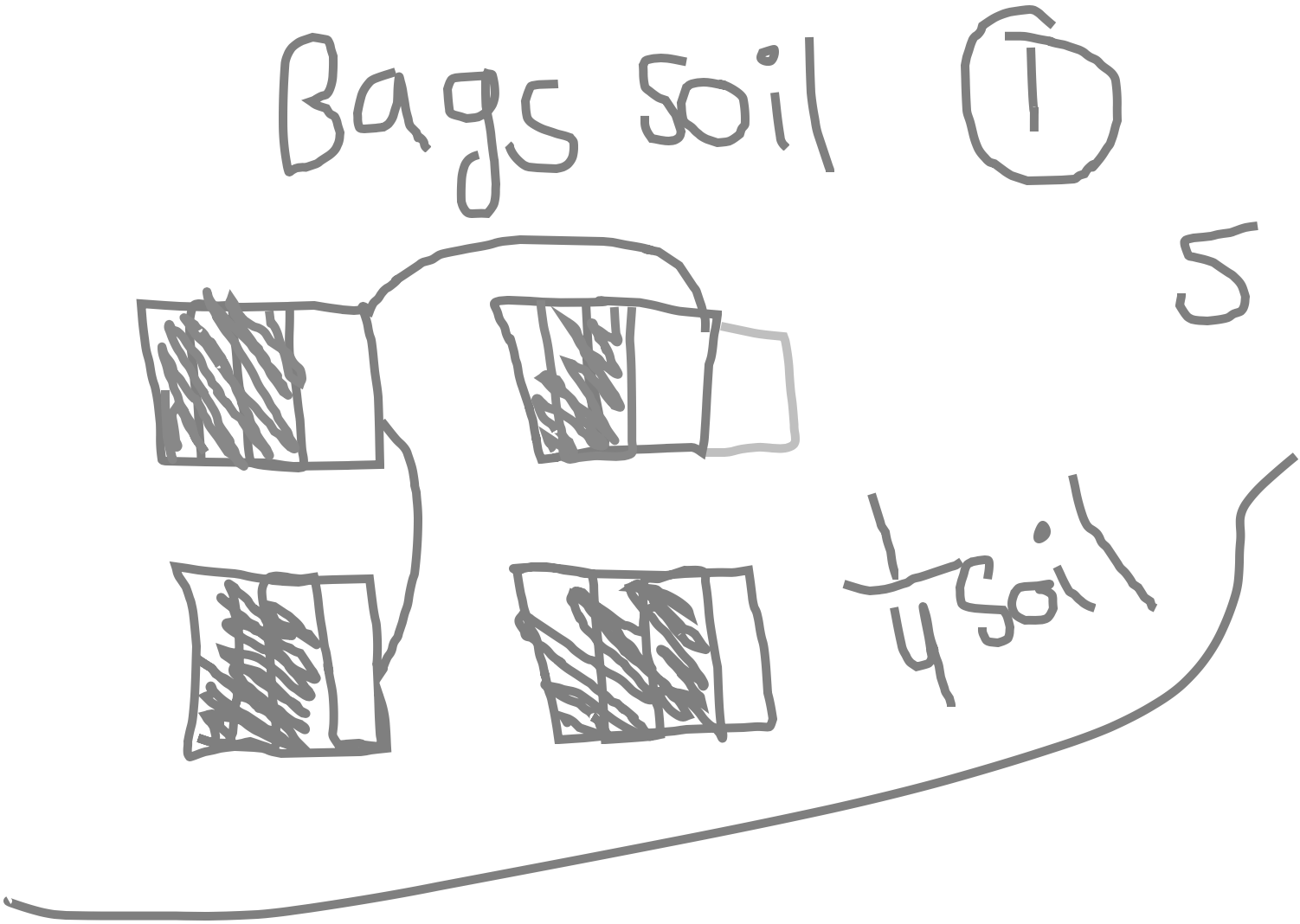
Such questions propel student thinking without significant load on language skills. Students who attempt to solve problems with only calculations leave teachers with less evidence of their thinking, depriving teachers of opportunities to advance ELs’ thinking through questions. These opportunities for explanation around diagrams are critical because they facilitate students’ mathematical understanding as well as their academic language development. For example, an EL produced the following work on a task about how many flower pots can be filled completely with 4 bags of soil if of a bag goes in each flower pot. The teacher asked what the “5” (upper right) meant, and after the student answered “5 flower pots,” asked the student to describe how the diagram helped show the answer of “5 flower pots.” Arguably, these opportunities for ELs to describe their thinking would not occur if only computational procedures were used.
How can we help students learn to use diagrams in problem solving?
Many middle-graders are not well versed in using diagrams, and this unit is designed to scaffold the use of diagrams for fraction division tasks through opportunities to create diagrams, analyze provided diagrams broken into steps, and analyze each other’s diagrams. All lessons are designed to focus on the importance of quantities and relationships. Questions are included throughout the lessons aimed at identifying quantities represented in student diagrams and relationships among quantities are spatially represented in their diagrams. Below is some additional guidance about supporting diagram use, in three categories: supporting students learning to use diagrams, supporting students using diagrams as thinking tools, and supporting students comparing diagrams.
- Students learning to use diagrams. We recognize that students may not be familiar with how to use diagrams when they start this unit. If students struggle to get started on diagrams, encourage them to “draw” or “show their thinking,” and as the unit progresses, there will be a continued focus on advantages of specific diagrams and how they can promote reasoning and communication. One approach to learning to use diagrams employed in these lessons is to have students analyze a fictional person’s attempts to use diagrams. The first example occurs in Lesson 1, and questions such as the following can support students in noticing how the diagram is set up may be helpful:
- What does the 4 represent in Step 1?
- What changes from Ella’s Step 1 to Step 2?
- Where on her number line do you see the size of one serving?
- Students using diagrams as thinking tools. As students use diagrams to support problem solving, help them reflect on how they have represented quantities and their relationships in diagrams. For example:
- Why did you partition your number line into six intervals?
- What does the number line represent?
- Where in your diagram is the number of flower pots that need filling?
- Students analyzing diagrams. Analyzing diagrams can help students notice quantities and relationships, as well support them in developing flexible thinking in their problem solving. To help students focus on key quantities and relationships in each diagram, ask questions such as:
- In Donna’s diagram, where do you see evidence that is larger than ?
- In Ben’s diagram, where do you see the amount of soil left over?
- Which diagram helps you to understand the problem?
Overview of ADSEL Lessons
Overview of lessons and mathematical ideas
The following chart presents a brief overview of the 8 ADSEL lessons:
| Lesson 1 | Lesson 2 | Lesson 3 | Lesson 4 | Lesson 5 | Lesson 6 | Lesson 7 | Lesson 8 |
|---|---|---|---|---|---|---|---|
| Ice Cream tasks | Flower Pot tasks | Flower Pot task | Speed task | Fish Tank task | Sharing Juice & Running tasks | ||
| Fraction division on a number line introduction | Measurement division problem solving | Partitive division problem-solving | Closing | ||||
The eight ADSEL lessons address four overarching mathematical ideas:
- A number line diagram can represent the quantities and relationships in a division task.
- Multiple diagrams can represent the quantities and relationships in a division task.
- Diagrammatic approaches can be used to determine a quotient.
- Equations can represent the quantities and relationships in a division task.
The following questions guide what students should be able to do successfully after the eight lessons: Are students able to:
- Use partitioning to precisely locate fractions on a number line?
- Identify the quantities given in a problem-solving context on a diagram (e.g., a number line diagram)?
- Represent the quantities from a measurement division task and a partitive division task on a diagram?
- Solve a measurement division task and a partitive division task using a diagram?
- Use a diagram to name the fractional part of a mixed number quotient in terms of another unit of measure?
- Identify connections between a diagram and a computational approach for a division task?
- Generate the division sentence that can represent a task?
Lesson structures
Each of the ADSEL lessons begins with a Launch, which includes use of the Three Reads strategy, and sometimes other strategies such as a Co-Constructed Word Bank. The launch serves to provide an opportunity to support students’ language access and to orient students to the mathematical work of the task. The launch closes with a few minutes of individual work time. Individual work time is important to allow students time to process that task and work independently before working with others. When students are working individually (or working with partners), do not assume that students need to complete the task before moving on to the next part of the lesson. A productive and engaging partner or full-group discussion about the mathematics can happen based on partially formed ideas. Give students enough time to get started, but they do not need to complete the task independently, particularly if other students have already finished.
Working with a partner is a regular part of each lesson, embedded in the main parts of the lesson (there are one, two, or three Parts in each lesson). In most lessons, after individual think time in the Launch, students share their thinking and their diagrams with a partner. Students also work on other parts of the lesson with a partner as working with a partner supports students in reasoning about their strategies and provides an opportunity for language production. Partner work is a key element of ADSEL lessons; in the section above on Supporting Student who are English learners, we emphasize how students benefit from working with partners. The opportunity to try out ideas with a partner and to hear what a partner has to say prior to a full-group sharing of ideas can build students’ confidence to speak in the full group and give them needed practice in talking about the mathematics before expressing the same ideas in the full group.
There are teacher check-in opportunities throughout the lesson, but in order to maintain the lesson flow and offer enough student work time, there is not a full-group teacher check in before and after every partner or individual work time. The lesson plans detail teacher check-ins and every effort should be made to keep these brief and get to the most important full-group check-in, which happens during the closing.
Each lesson has a Closing, where the teacher can review the key ideas of the lesson in the context of another example or a fictitious student’s work. The closing has time for the teacher and students to share their thinking. The lesson plans describe how to lead each closing discussion. The closing discussion, similar to the launch, is a combination of full group discussion and partner or individual work. Make sure to have students who are ELs have frequent opportunities to be the ones to share their work during the closing (and during full-group check-ins throughout the lesson).
As the ADSEL lessons include a mixture of individual work time, partner work, and full group sharing and discussion, icons included in the Student Book help students identify how each part of the lesson should be completed:
| Individually | Partners | Full Group |
|---|---|---|

|

|

|
Activity types
In addition to frequent opportunities for students to create their own diagrams and discuss how to use them to solve fraction division tasks, ADSEL lessons employ two other main activity types to support student learning: worked examples and matching tasks.
The ADSEL lessons use a form of worked examples to present a problem-solving approach to a task as a means to support students in developing more flexible understandings of fraction division and in seeing the affordances and constraints of different diagrams. For example, Lesson 3 presents the work of Teresa, a fictitious student who solves the Filling Flower Pots task, and this worked example provides an opportunity for students to analyze Teresa’s steps in her problem-solving approach. This sort of analysis can focus students’ attention on specific mathematics concepts or skills, can present a problem-solving approach, and can provide an opportunity for students to carefully reflect on different steps in solving a task. Research shows that students develop more flexible thinking when it comes to problem solving when they compare different solution strategies on the same task. The worked examples in this unit are organized with sentence starters to support students’ analysis. Sentence starters can encourage students to use academic language they may not otherwise use and support students of different language proficiency levels to participate in verbal and written mathematical communication.
Lessons 5, 6, and 8 use matching tasks that ask students to match tasks to diagrams and equations. Students have the opportunity to use the information provided and do not need first to solve a task or write the answer. Instead, they can focus on their explanations and their reasoning. In this manner, matching can help promote mathematical discourse because the emphasis is on explaining why (or why not) particular cards belong in particular categories. During matching activities, all students should have the opportunity to explain their thinking to a partner and students should also discuss why they agree or disagree with their partners about which task matches which diagram or equation.
Supports for Students who are English Learners
What language strategies are emphasized in the unit?
Language support strategies can reduce some of the linguistic demands inherent in mathematical communication. Students benefit from these strategies in the context of the mathematical work, that is, not only as strategies that happen outside of the mathematics task but strategies that happen during their engagement in a mathematical task. A focus on the overarching mathematics, in this case fraction division, even when working to support language, allows students to develop their understanding of the mathematics as they gain English proficiency.
Our 8-lesson unit integrates several strategies, including: Three Reads; Acting Out; Co-Constructed Word Bank; Sentence Starters and Frames; Revoicing; and structured Partner Work. The Three Reads and Acting Out are language access strategies while the Co-Constructed Word Bank, Sentence Starters and Frames, and Partner Work are primarily language production strategies. In our experience, these strategies work well in concert. In these materials, we have integrated these strategies into lessons to support students understanding and participation. These strategies can be further tailored with consideration for the English language proficiency levels of students or for the mix of first languages that are present in a given class. Further description of how to implement each strategy is found in the next several sections of this document.
What is the Three Reads Strategy and how should it be implemented?
The Three Reads strategy is a language access support that can facilitate sense-making of mathematics text such as word problems during the launch or sense-making when introducing a new task. It consists of three structured readings of a mathematics task with a different purpose and focus during each read. It facilitates the process of understanding the meaning in word problems, thus boosting access for English learners, and in the ADSEL lessons it specifically supports students in linking task information to their work on drawing or analyzing a diagram.
Rationale. Reading a word problem requires a different approach than reading prose, in part because the purpose (e.g., the question to be answered) typically does not appear until the end of the passage. Since the reader does not know the purpose until the end, it can be difficult to determine the importance of the information within the text. In addition, math problem text is often dense and may include unfamiliar academic language, complex long sentences, or unfamiliar ways to express relationships. Reading it more than once may strengthen students' understanding of a text. A focus on the mathematical context, rather than the specific vocabulary, grammar, or sentence structure, also supports students in building upon the mathematical skills and concepts they already know.
Implementation. Although the Three Reads strategy can be successfully used individually or quietly, repeated reading out loud in a small group or whole class provides additional support to ELs by providing opportunities to hear and see the language multiple times. In each lesson, we present the Three Reads Strategy on the first page of the lesson, and there is a prompt to complete after each read focused on the purpose for that read:
The Gardener's Flower Pots
The gardener had 6 bags of soil for her flower pots.
Each flower pot needs of a bag of soil. How many flower pots can she fill?
Complete the Three Reads for The Gardener's Flower Pots
1st Read - Context
The problem is about...
2nd Read - Purpose
I need to find out...
3rd Read - Information
The important information is...
- The first read is to get a sense of context in order to understand the "story" or context of the text. Students should not focus on the quantities or relationships between them during this reading. Responses should be more like a title for the problem, such as “Ice cream,” “Sharing ice cream,” “flowerpots and soil”. Students complete the sentence, “The problem is about….”.
- The second read is to discern the question or the goal of the task. The problem is read again in its entirety, looking specifically for information about what needs to be answered, or if there is no question in the task then what the students are supposed to do. Students complete the sentence starter, “I need to find out…”. Focus students on what they need to find out for a final answer, and not just an operation (for example, encourage, “I need to find the number of servings,” rather than, “I need to subtract/divide”).
- The third read of the text is to gather important information that is needed to solve the problem or achieve the purpose of the task, such as specific quantities and their relationships. Students complete the sentence starter “The important information is…”.
After each read, provide students with brief think time to complete the prompt, and then have a couple students share their responses. Having multiple students share allows all students to hear the information and compare it with their ideas and ensures that more ideas are on the table and promotes connections between different ways of phrasing the ideas (e.g., running laps and ran laps). Record students’ responses and indicate which pieces of “information” shared for the third read are correct or important to keep in mind before moving on to working on the task.
The information from the third read should be used as students draw a diagram or do the next step in the lesson. In the lessons, we explicitly prompt students, for each task, to draw a diagram that captures the important information (of the third read). This is a critical step that supports students in linking the important information from the task to the mathematical work that students need to do to solve the task. Remind students to reference what they did in the Three Reads as they work on the task individually or with a partner.
How and why should you act out mathematics tasks?
Rationale. Students can benefit from seeing a math task in action. Acting out tasks supports ELs in interpreting text because they are able to watch an enactment of the task context while hearing the language in the task. This active visual demonstration allows ELs to both hear and see the language used. For example, by acting out pouring soil into flower pots (for Lessons 3, 4, and 5), students can develop an understanding of the problem context. The use of real objects, such as flower pots and soil (or sand), can help students interpret the problem context and learn vocabulary by seeing and experiencing "hands-on" objects represented by words in the problem context.
Implementation. Acting out can be integrated with the Three Reads strategy by acting out the task scenario during the first or second read of that task, or immediately after reading the task and before asking students about what the problem is about or what they need to find out. Then, students should complete the prompts in the Three Reads template. Note that videos or pictures can also be used in place of acting out in some cases if acting out is not possible.
To prepare to act out a math task, think through which part of the task makes sense to act out and what information you want to highlight. For example, while both Lesson 3 and Lesson 5 involve flower pots, the acting out of the task would be very different. Review the tasks below and think through how acting out the tasks would be similar and different for the two lessons because of what is known and what is unknown:
| Task and important information | Task objective |
|---|---|
| Lesson 3: Filling Flower Pots
Grandma has 4 bags of soil for her flower pots. Each flower pot needs of a bag of soil. How many flower pots can she fill? |
Known: amount of soil for each pot
Unknown: how many pots can be filled? |
| Lesson 4: The Gardener’s Flower Pots
The gardener has 6 bags of soil for her flower pots. Each flower pot needs of a bag of soil. How many flower pots can she fill? |
|
| Lesson 5: Red Flower Pots
5 bags of soil fill 4 red flower pots. The red flower pots are all the same size. How much soil is in each red flower pot? |
Known: number of flower pots; amount of soil
Unknown: how much soil goes in each pot? |
In the Filling Flower Pots tasks and in the Gardner’s Flower Pots task, the objective is to determine how many flower pots can be filled, but in the Red Flower Pots task, there are 5 bags of soil and 4 red flower pots, and we need to determine the amount of soil needed for each pot. Because the task objectives and what is known (and what is unknown) is different across the tasks, the tasks will be acted out differently. (The lesson plans for Lessons 3 and 5 provide specific guidance.)
How is the Co-Constructed Word Bank different from a typical word wall?
Rationale. The Co-Constructed Word Bank is a language production support for ELs to make sense of mathematics text that is in a word problem and then use that mathematical language in their speaking and writing. Similar to other types of “word banks,” the Co-Constructed Word Bank:
- Keeps important words visible for students throughout a lesson for students to use.
In contrast to more generic word walls, a Co-Constructed Word Bank:
- Includes phrases and terms related to the problem context or task.
- Specifically includes terms that both teachers and students raise during discussions as being important or potentially confusing.
In this manner, a Co-Constructed Word Bank facilitates ELs’ language production by providing them with access to mathematical language that they can use to communicate with others about the math task and their mathematical reasoning. When teachers ask students to use particular words or phrases from the Co-Constructed Word Bank, they are prompting students’ language production and providing opportunities for students of different English proficiency levels to use rich mathematical language.
Implementation. The Co-Constructed Word Bank is usually generated during the launch of the problem—usually after the third read in the Three Reads Strategy—with students bringing up phrases and terms that are in the problem or that they think they may use in their discussion of the problem and the teacher adding any additional important or potentially confusing words or phrases.
In our lessons, a Word Bank box is frequently placed in the third read of the Three Reads template, and also in spots later in the lesson when other words may need to be defined. While the word bank should be co-constructed by students and the teacher, the Co-Constructed Word Bank is labeled as a “Word Bank” in the student materials to facilitate student access and avoid unnecessary language.
Word Bank:
serving
equivalent
total
3rd Read - Information
The important information is...
A Co-Constructed Word Bank can also be populated later in a lesson when academic language used to engage in learning, such as verbs like “justify,” are introduced to students.
justify
10. Justify which number line you and your partner chose:
- How does the number line show the important information?
- How could you use the number line to solve the task?
While co-constructing the word bank with students, teachers can highlight and clarify terms or phrases that they determined ahead of time need clarification to support students’ understanding and communication. The teacher can also ask students to try to use particular words from the word bank in their discussions with partners or written explanations.
How do sentence starters and frames support mathematical communication?
Rationale. Sentence starters and frames are useful in eliciting student self-explanations about the what and the how of their solution steps—and why they used those steps. Sentence starters and frames are a language production strategy that can support students as they craft and share their mathematical ideas verbally and in writing. Sentence starters and frames are incomplete sentences that students are asked to complete and which provide structures for students’ writing and speaking—sentence starters provide the beginning of a sentence, while sentence frames provide the beginning of a sentence as well as some later part of the sentence, asking students to fill in the missing parts. When given a sentence starter or frame, a student can spend less time interpreting a question and can instead focus on formulating their ideas. For example, in Lesson 3, we ask, “Why did Teresa divide each rectangle into four equal pieces?” and then we provide a sentence starter: “Teresa divided each rectangle into four equal pieces because…” Sentence starters can encourage students to use academic language they may not otherwise use or support them using a specific academic term, phrase, construction, or pairs of terms that go together mathematically. Sentence starters and frames can also facilitate students’ explanations and sharing, even with non-academic language. A variety of sentence starters can accommodate a range of English proficiency levels. A sentence starter crafted for students with lower English proficiency levels may provide opportunities to practice using language while requiring that students complete the sentence using only a word or two. Sentence starters crafted for students with higher English proficiency levels may include more sophisticated sentence structures or more challenging words, phrases, or constructions and/or require longer responses.
Implementation. There are sentence starters and frames built into the lesson materials, for example, during the Three Reads Strategy, analysis of student examples, problem-solving tasks, and the closing. Encourage students to complete the sentence starters and think of sentence starters as an opportunity to begin to share their thinking. Remember that students are working to develop understanding of how to share their ideas, and therefore, their completed sentence starters should be considered “rough drafts.” Sentence starters present what students are thinking and might say, but as written may not be spelled correctly or may use informal language. There are multiple correct answers to the sentence starters and the purpose is not to evaluate student thinking during their partner work but support students in attempting to communicate mathematically, even in imperfect ways. In that manner, think of students’ completed sentences as an opportunity to see their mathematical thinking and encourage language production, not perfect responses.
The lessons also make use of Sentence Starter Cards to support student mathematical communication during partner work. The cards are introduced in Lesson 1 when students are sharing their diagrams with their partners—and during Lesson 1 there are instructions for having student volunteers model how to use the sentence starter cards as they will be used in every lesson.
| This diagram shows... | In this diagram, I see... | In this diagram, I don't see... |
| This diagram helps me see... | I like this diagram because... | I wonder where... |
How and why should you revoice what students say during a mathematics lesson?
Rationale. Revoicing is a strategy for adding or seeking clarity about what students are saying and for introducing academic language in a way that builds on and connects to students’ own mathematical thinking. It involves repeating or rephrasing what students say about the mathematics and thus requires careful attention to what students are saying or doing so that any restatements of student talk honor the content of those students’ ideas. Revoicing can be a useful tool for adding clarity to a discussion, highlighting particular ideas from students or making connections among those ideas, and building academic language and patterns of talk into the discussion in ways that build off students’ own ideas and the ways they have expressed these ideas.
Implementation. Revoicing can be used throughout a lesson from the initial launch of the task through to full group discussions. In the ADSEL lessons we highlight opportunities to carefully consider how to use revoicing during full group sharing. Below are several tips to consider when using revoicing:
- The timing of revoicing is critical to consider. Do not interrupt a student in the midst of a train of thought in order to re-state or clarify something they said if it will get in the way of their active thinking. Instead, find natural pauses in a student’s explanation or in the discussion to clarify or restate what students have said.
- Honor and affirm students’ ideas (whether fully correct or not) through the revoicing process. When you restate a student’s idea, you are highlighting how it is productive for the student to have voiced that idea because regardless of whether it seems to be complete thinking, it can help move the student and the class forward by considering that idea.
- Encourage student talk about the mathematics while also promoting precision by using revoicing strategically. When there is important academic language to be used in a lesson, rather than waiting for a student to be able to come up with exactly the right word and passing by alternative descriptions of the concept, encourage and accept more informal descriptions of the concepts from the students in order to promote that thinking, and then add to it by revoicing the idea in ways that bring in more precise language and male a claim more precise (for example, if a student says that multiplication makes the result bigger, ask them when that is the case). Revoicing is not about correcting students but about helping to add clarity and precision to the ideas and claims that students are generating themselves.
- Ask students to revoice each other’s ideas. Giving students opportunities to re-state in different ways what their peers have explained facilitates additional opportunities both for understanding and for language production.
Why is partner work a support for students who are ELs and how should it be implemented?
Rationale. Partner work is critical to supporting student language production because more student talk happens in small group or partner work than in a full group discussion. Students who are ELs can benefit from a language rich environment in mathematics teaching and learning, and partner work provides an opportunity for all students to share their thinking. In addition, the opportunity to try out ideas with a partner and to hear what a partner has to say prior to a full-group sharing of ideas can build students’ confidence to speak in the full group and give them needed practice in talking about the mathematics before expressing the same ideas in the full group. The partner work that we envision reflects the following set of values about learning mathematics that we want all students to internalize and act on:
- Listening to how others think about a problem is important for my learning and for theirs.
- The process of explaining how I think about a problem is important for my learning and for others’ learning.
- Everyone deserves time to make sense of mathematics problems.
- The process of challenging unreasonable mathematical claims is important for everyone’s learning.
- Proficiency in English is not a prerequisite for sense making, explaining, listening, or challenging reasoning.
While these values do not need to be made explicit to students, this last value statement is particularly important as a guide for teachers of English learners.
Implementation. Every lesson in the ADSEL unit includes extended time in pairs for mathematical work and discussion as partners. A first consideration is how you will place students into partnerships. You can put students into partnerships using many different strategies, but it is important to be intentional and to teach all students to be a good partner (Chval, Pinnow, Smith, & Perez, 2018). Whenever grouping students, it is important to attend to the academic strengths of students, and also to their English language proficiencies and the goals of the lesson. A classroom environment that supports all students, including ELs, as competent mathematical thinkers is critical to productive partner work. Make sure that all students create a space for each other’s thinking and learning. It is important to ensure that it is clearly defined who each student’s partner is so they know who to work with and so the two students can take joint responsibility for working on the task. Try to avoid having larger groups of students working together, where individual students may get lost and not have as many opportunities to express their thinking and talk about the mathematics.
Once you have established partnerships, keep in mind that mutually beneficial partnerships do not happen automatically. Sometimes, with the best of intentions, peers may assume that the best way to “help” an EL student is to dominate the discussion. If that happens, teachers should position the EL as a competent thinker and not as an individual in need of help. Below are some additional tips for helping students make the most of the discussion time:
- Individual time prior to moving into pairs or small groups can allow students to start to develop their own mathematical ideas, which can then fuel discussions with partners or small groups.
- Regularly remind students of the communication norms/rules.
- Act in ways that position ELs as competent mathematical thinkers and communicators, for example by focusing on what they do well rather than their mistakes or noting when an EL has contributed an important mathematical idea or when an EL has expressed a new idea that had not come up before in the discussion.
- Model questions that can help partners, especially questions that refer to diagrams the students are discussing.
- Guide students to the questions in the Student Book to guide their conversation, and have them use the sentence starters and frames listed in the student book as well as the Sentence Starter Cards to focus their talk on the mathematical work of the task.
- Watch for unhelpful communication patterns between partners and suggest alternative ways of communicating.
- When students are working with partners, do not assume that students need to complete the task before the sharing of ideas happens in the full group. A productive and engaging full-group discussion about the mathematics can happen based on partially formed ideas.
The following table presents possible communication rules and detail how teachers may support student-to-student communication between partners:
| Norm and rules of communication | Teachers supports for student communication |
|---|---|
| Everyone shares mathematical thinking with partners |
|
| Listen carefully when your partner shares their mathematical thinking |
|
| After listening, ask questions that might help your partner’s thinking |
|
| Challenge unreasonable mathematical thinking |
|
Understandings of Fractions and Division
Why is fraction division an essential topic for middle grades mathematics?
Investing adequate time in learning fraction division can facilitate students’ understanding of a wide range of mathematical content in sixth grade and beyond. For example, work with fraction division helps to solidify students’ understanding of fraction operations more generally. The expression 8 ÷ 5 is more than a call for implementing a computational procedure; it is a statement of the multiplicative relationship between 8 and 5. Understanding how two numbers are related to each other multiplicatively is an essential prerequisite to proportional thinking and to success in algebra.
In addition, fraction division touches all of the rational-number content that is covered in sixth grade. For example, under the topic of ratio, if you want to check quickly that 9:8 and 2: 2 are equivalent ratios, you may want to convince yourself that 9 ÷ 2 = 4, since 8 ÷ 2 = 4. Under the subtopic of unit rates, the unit rates for an 8:3 rate are 1: and : 1, and and are inverses of each other. This inverse relationship holds for all unit rates. Also, in the topic of proportions, one way to find a rectangle with short side 5 that is similar to a 9 x 8 rectangle is to calculate 8 ÷ 5 and multiply that number times 9.
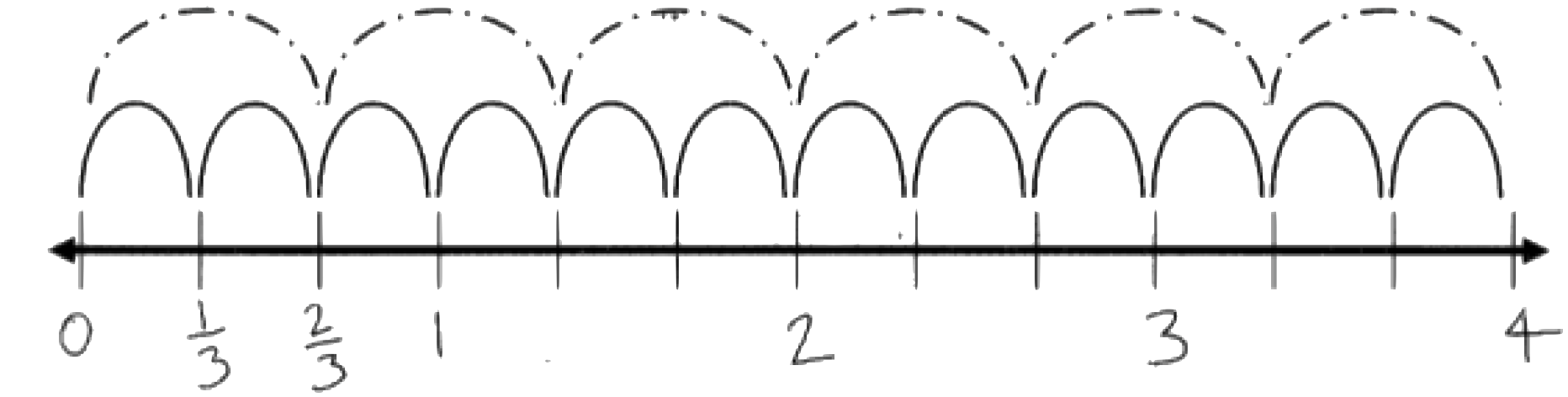
Why is it important for students to know how to locate fractions on a number line?
The beginning of this unit includes attention to foundational understandings that can support the work around division of fractions by fractions. Lessons 1 and 2 provide an opportunity to review foundational fraction content such as fraction magnitude that can support the work around fraction division. Students need to have foundational knowledge of fractions to be able to engage successfully in fraction problem solving, which includes being able to visualize fractions, being able to compare the fractions, and understanding the why along with the how in fraction computation. Students need multifaceted and flexible knowledge and understanding of fractions for success with fraction division.
Research suggests that it is specifically important that students understand fractions as numbers with magnitude. Understanding fractions as numbers with magnitude means understanding fraction ordering is an extension of whole number ordering. In a fraction, the numerator and denominator work together to determine the magnitude of a fraction, and fractions are magnitudes that can be represented on a number line. It is important for students to expand their understanding of fractions as numbers (as opposed to a pair representing parts of a whole) and to do so in ways that are not just symbolic. For example, the fraction is more than a way to represent “two parts out of three.” It also represents a number whose size can be compared with other numbers, with students knowing, for example, that is larger than and less than , and recognizing that this can be demonstrated on a number line.

To order fractions and place fractions on a number line in relation to other fractions, students need to consider both the numerator and denominator of a fraction and the number size of the fraction. Research has shown that understanding that fractions can be represented on a number line provides an underlying structure for learning a range of fraction concepts and skills.
What is measurement division? What is partitive division? Does it matter?
In mathematics, a division expression like 54 ÷ 5 has one and only one meaning—it is the number that produces 54 when multiplied by 5. In real-world contexts, however, there are two meanings depending on context.
Measurement division is a way of understanding division in which you divide an amount into groups of a given size and you want to know how many groups you can make. An example of a measurement division task is: You have 12 yards of cloth. It takes 2 yards of cloth to make one dress. How many dresses can you make? In this example, you are dividing a given amount (yards of cloth) into a given size (2-yard pieces) and need to determine how many of those pieces will fit into the given amount.
Partitive division, or sharing division, is when you have a given amount and a set number of groups and would like to determine how much is in each group. An example of a partitive division task is: You have 12 yards of cloth. You would like to make 8 shirts. How much cloth would you have for each shirt? This is the same as finding the unit rate, in this case, yards per shirt.
It is not necessary for students to identify these two different understandings of division by name; rather, students need to be able to understand and solve a variety of division tasks and therefore, they need rich problem-solving experiences in a variety of division contexts.
The ADSEL materials begin with a focus on measurement division, where the size of the part (or portion or serving) is known. Lessons 1 and 2 include tasks about how many servings of ice cream are available given an amount of ice cream and a serving size, and Lessons 3 and 4 include tasks about filling flower pots with soil where the amount of soil and soil per pot is known. Lessons 5 and 6 includes partitive division tasks, where the number of groups is known, but the problem solver needs to find the size of each part. Specifically, in Lesson 5 there are a certain number of flower pots and a set amount of soil, and the objective is to determine how much soil per flower pot, and in Lesson 6 there are questions about speed where the number of miles and the number of hours are known but not the number of miles per hour. The chart below illustrates the difference for the Flower Pot tasks in Lessons 3, 4, and 5.
| Task and important information | Task objective | Type of Task |
|---|---|---|
| Lesson 3: Filling Flower Pots
Grandma has 4 bags of soil for her flower pots. Each flower pot needs of a bag of soil. How many flower pots can she fill? |
The amount of soil needed for each pot is known, and the objective is to determine: How many flower pots (or fractional pots) can be filled? | Measurement division task |
| Lesson 4: The Gardener’s Flower Pots
The gardener has 6 bags of soil for her flower pots. Each flower pot needs of a bag of soil. How many flower pots can she fill? |
||
| Lesson 5: Red Flower Pots
5 bags of soil fill 4 red flower pots. The red flower pots are all the same size. How much soil is in each red flower pot? |
There are a certain number of flower pots and a given amount of soil, and the objective is to determine: How much soil can go into each flower pot? | Partitive division task |
How do we facilitate student understanding of the quotient and what is the role of diagrams?
Understanding the quotient in a division task can be challenging. Students need to be able to explain what the quotient means in the problem context, and supports are built into the lessons to help students learn how to do so. First, let’s look at an example of a partitive division task, where the explanation can be a little more straightforward:
You have 12 yards of cloth. You would like to make 8 shirts of the same size. How much cloth would you have for each shirt?
The numerical answer, 1, designates the yards of cloth for each shirt. The yards of cloth were divided equally, and the quotient inherits its label from the dividend.
Understanding the quotient can be especially challenging in measurement division tasks. An example measurement division task is:
You have 12 yards of cloth. It takes 5 yards of cloth to make one large dress. How many dresses of the same size can you make?
The numerical answer of 2 can be challenging to interpret. The 2 refers to the number of dresses. The 2/5 raises the question, “ of what?” Students may be tempted to say of a yard, but it is of a dress can be made. In measurement division, the quotient inherits its label from the divisor, in this case, dresses that can be made, that is, we have 2 dresses. Interpreting the fractional part of a mixed number quotient in measurement division tasks, or “remainder,” is a skill that is addressed in Lessons 3 and 4. In Lesson 3 students analyze the following diagram (Teresa’s diagram) for the Filling Flower Pots task, and discuss how the leftover soil (shown in this diagram as one small rectangle not enclosed by a heart-shaped loop) is equal to of a bag of soil at the same time that it is equal to of a flower pot.
| Filling Flower Pots Grandma has 4 bags of soil for her flower pots. Each flower pot needs of a bag of soil. How many flower pots can she fill? |

|
A number line diagram can also be an effective tool for supporting student reasoning about the quotient. In Lesson 4, students analyze a series of “Jason’s” diagrams for the Gardener’s Flower Pots task, and in the diagram shown below they consider how a bag of leftover soil is the same as of a flower pot that can be filled with that leftover soil:
| The Gardener's Flower Pots The gardener has 6 bags of soil for her flower pots. Each flower pot needs of a bag of soil. How many flower pots can she fill? |
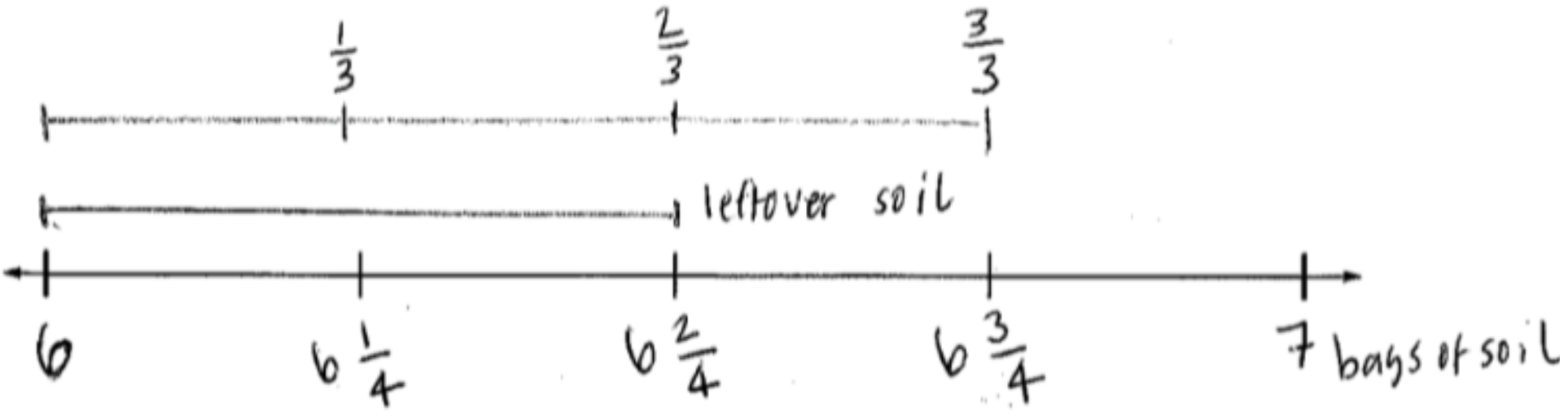
|
What is the unit’s perspective on learning a computational procedure like “invert and multiply”?
Most of us learned a procedure in school for calculating division by fractions. As mathematics educators, we probably still use the procedure occasionally, if not frequently. We also recognize that some of your students may come to your classroom with knowledge of, or at least awareness of, a calculating procedure for fraction division. There is no doubt that “invert and multiply” (or a comparable procedure) is a handy tool to have, especially when the numbers in a fraction division task are not very friendly. You may choose to take time to help other students learn a computational procedure. However, while our unit will acknowledge and introduce computational procedures in lesson 7, the unit will not spend much time on computational procedures. Our intention is for students to learn approaches that give them other options in thinking about fractions and division, in particular, the use of diagrams to solve division problems. Following are two primary reasons to believe that reliance on computational procedures alone for fraction division is insufficient, in addition to the many other benefits of work with diagrams noted earlier in this document.
- Sometimes, word problems do not shout out “fraction division” to students (even when fraction division would be a useful in finding a solution) or do not seem to be associated for students with the computational procedure they have been taught. In this case, they are left on their own to decipher the problem statement and context then solve the task. Often, they will resort to an inappropriate computational procedure and go off track from what the problem is asking. An example task that many students may not see as a division task follows:
Red Flower Pots
5 bags of soil fill 4 red flower pots. The red flower pots are all the same size. How much soil is in each red flower pot?Some students will immediately see this as a “division” task and divide 5 by 4. Many others will not and are more likely to approach it as a “sharing” task, distributing the 5 bags diagrammatically, as this student does:
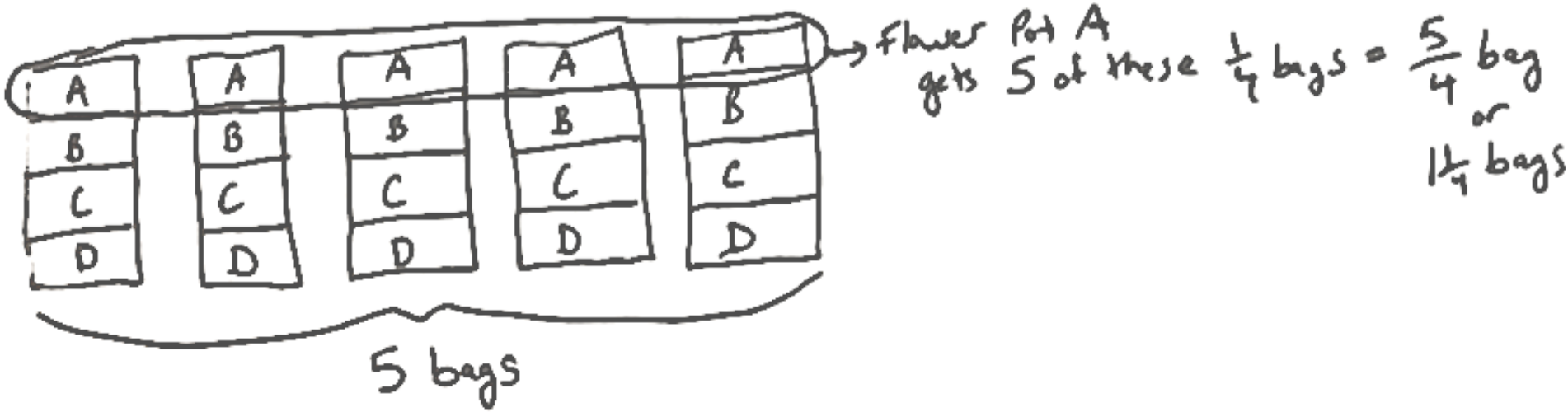
This student distributed of each of the 5 bags of soil into one flower pot, and combined the five s to equal bag, then repeated with the other -parts of the bags. It is likely that this student would not see a connection between this and the learned computational procedure for division. The point is: it is risky to give students “invert and multiply” (or another such procedure) as their only tool for fraction division, since they may not know when to call it into play. It is far better that they have not only the computational tool, but also the capacity to think with diagrams about a word problem’s solution. Diagrammatic approaches can back up calculation tools, provide meaning for a computation, and encourage flexible thinking.
- Diagrams often reveal more about the task than a computational procedure. One task in Lesson 3 is: “Grandma has four bags of soil for her flower pots. Each flowerpot needs of a bag of soil. How many flowerpots can she fill?” In response, one student who was an EL drew the following diagram:

He told the teacher: “She can fill 5 flower pots. She has of a bag of soil remaining.” The teacher asked: “How much of a flower pot did she fill with the remaining soil?” The student was able to use the part of his diagram labeled “5” to see that the unmarked quadrant is both 1/4 of the entire bag, and 1/3of the marked quadrants. He answered correctly: “ of a flower pot.” In the student’s diagram, we can also see other relationships, which other students might notice if given the opportunity to analyze the diagram: e.g., that the fourth loop that the student drew does not include any soil from the fourth bag of soil, which is evidence that divides into 3 evenly 4 times. Relationships such as this can show up in a diagram, but rarely in a computational approach to this task.
Computational Approach in ADSEL Lesson 7. A computational approach is presented in Lesson 7 when a fictitious student, Lin, uses an invert and multiply algorithmic approach to the Fish Tank task. We introduce this method because it is one that many students may already have encountered or will likely encounter at some point. The goal in this lesson is not for students to become adept at using Lin’s method. However, by making sense of Lin’s method and working to connect it to Jenny’s diagrammatic approach, students can begin to see that these are both useful methods of working on the same problem. Students will begin making those connections by identifying how the different quantities from the problem are represented in both Lin’s and Jenny’s approaches when solving the Fish Tank task:
Fish Tank
10 gallons of water fill of a fish tank. How many gallons of water completely fill the fish tank?
Jenny’s number line diagram in Lesson 7 shows the 10 gallons are divided into three (to show how many gallons are in each fourth of the tank) and then multiplied by four (because there are four fourths). In this manner, ten divided by 3 and multiplied by 4 can be seen in Jenny’s diagram. In Lin’s approach, seeing it as 10 divided by 3 and multiplied by 4 depends on understanding 10 x as being the same as 10 x 4 x or 10 x x 4 and seeing multiplying by as being the same as dividing by 3. While we present this opportunity for students to see the invert and multiply algorithm for fraction division in Lesson 7, we believe that it is critical for students to learn that they can always draw a diagram to reason out division tasks, and that both diagramming and computational procedures, if done correctly, will result in the quotient.
What is the role of division and multiplication sentences or equations in the lessons?
Relationships are the lifeblood of mathematics, and it is worthwhile for students to associate multiplication and division. Initially, to support students in thinking through representing situations flexibly, early lessons begin with presenting a division sentence with the student work on a task. For example, in Lesson 3, Teresa’s approach on the Flower Pot task begins with a division sentence to represent the Filling Flower Pots task, written in Teresa’s handwriting:

We present a fictitious student’s work as a means to show how a task might be identified as relating to a division sentence/equation, and to encourage students to generate a multiplication or division sentence themselves. Then, in subsequent lessons, such as in Lesson 4, we prompt students to write a division sentence or to match a given division sentence to mathematics task, such as in Lesson 5:
|
3. Write a division sentence using the important information from The Gardener's Flower Pots task. You do not need to calculate the solution. ÷= ? |
What division sentence below matches the question: How much soil fills each blue flower pot? 4 ÷ 5 = ? 5 ÷ 4 = ? |
Furthermore, seeing the relevance of multiplication to solving the task can help students see both multiplication and division as options for the same task. Most students see multiplying and dividing as inseparable partners, and understanding this partnership provides students with options when understanding task contexts and when solving tasks. For example, the Fish Tank task, introduced in Lesson 7, can be approached as a division task (10 ÷ = ?) or as a multiplication task ( x ? = 10), or even as a unit rate task (amount of water per fish tank).
Fish Tank
10 gallons of water fill of a fish tank. How many gallons of water completely fill the fish tank?
In addition, this task offers an opportunity for students to consider representing times an unknown number. Students could solve the task algebraically, x ? = 10; few sixth-graders, however, would represent this as an algebraic equation. In our experience, diagramming is an approach many students use to exploit the visual nature of the task and to represent both the amount of water and the fractional tank. For example, this student envisioned the tank as a rectangle and divide it into fourths:
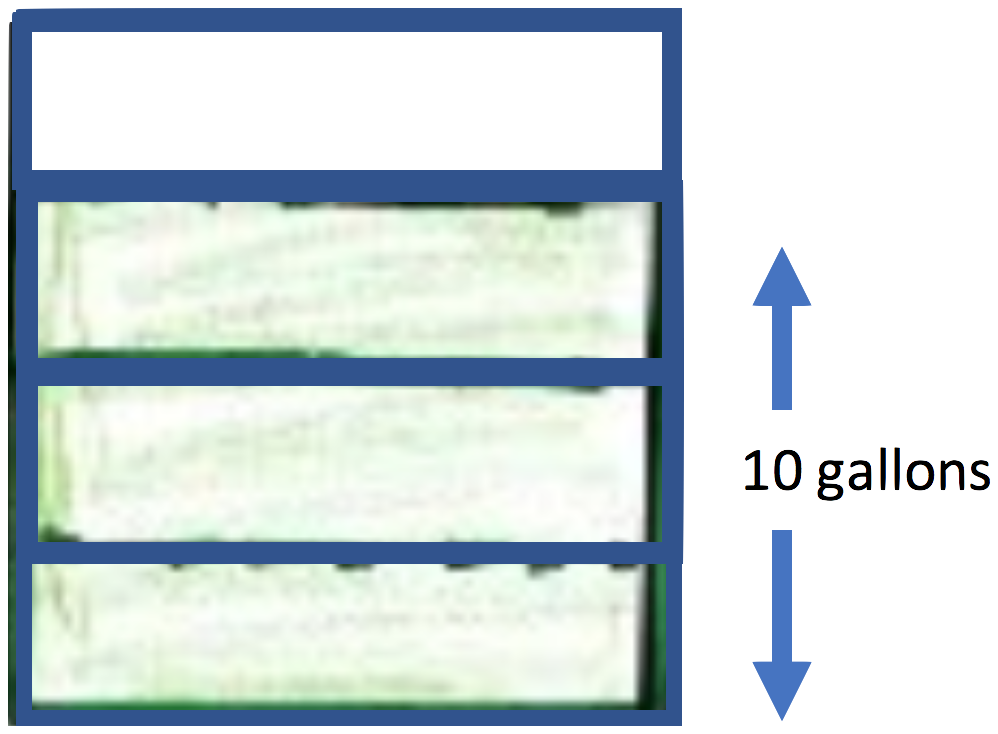
This student divided the rectangle horizontally in order to preserve the visual representation of water in a tank. A diagram support students to represent a task as both a multiplication task, where x ? = 10 is shown with shading, and as a division task, 10 ÷ = ?.
Having the flexibility to frame a situation as either division or multiplication benefits problem solvers because they can choose an approach that makes sense to them. Furthermore, when we do not emphasize the relationship between multiplication and division, students may develop the belief that fraction division exists in a region of “doing math” that is totally divorced from the region in which multiplication exists. Being aware that a division equation can be re-written as a missing-value multiplication equation is valuable in solving problems and to recognizing relationships.
Lessons 1 & 2: Ice Cream Tasks
Fraction division on a number line introduction

Lessons 3 & 4: Flower Pot Tasks
Measurement division problem solving

Lessons 5, 6, & 7: Flower Pot, Speed, & Fish Tank Tasks
Partitive division problem solving

Lesson 8: Sharing Juice & Running Laps Tasks
Closing

The Analyzing Diagrams: Supports of English Learners project is supported by the Institute of Education Sciences, U.S. Department of Education, through grant #R305A170297 to Education Development Center. The opinions expressed are those of the authors and do not represent views of the Institute or the U.S. Department of Education.

|
© 2022 Education Development Center, Inc. All rights reserved. Analyzing Diagrams: Supports for English Learners (ADSEL) |